Indice
disegnare  > assonometria  > punto di vista
Come definire il punto di vista assonometrico


La rappresentazione assonometrica, appunto perché proiezione parallela, è un metodo di rappresentazione che conserva inalterati i rapporti angolari e dimensionali. Il termine stesso, assonometria, indica che le misure dell'oggetto sono riportate direttamente sugli assi.
Viste


Proiezione assonometrica di un cubo su un piano con angolo
di 30 gradi. Il centro di proiezione è all'infinito e i raggi sono
paralleli.

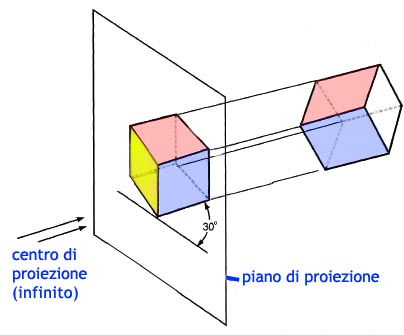
Sistema di riferimento

L'oggetto viene rappresentato in modo facilmente comprensibile, in quanto riunisce più viste in un solo disegno, con dimensioni corrette o proporzionate.

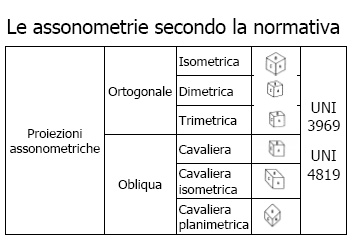
Tipi di assonometria secondo la normativa UNI 3969 e UNI 4819
 

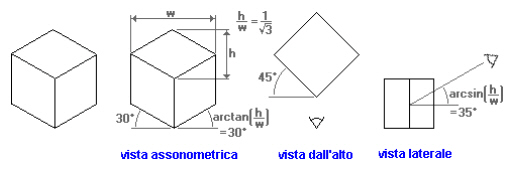
Gli assi proiettati presentano un fattore di riduzione dovuto al fatto che non sono paralleli al piano di proiezione. Il fattore di riduzione (detto scorciamento) è di 0.816 rispetto alla grandezza reale. L'angolo tra gli assi è di 120 gradi.

Vista di un cubo in assonometria isometrica.
L'angolo di vista in pianta è di 45° e di 36° in altezza.

 

In AutoCAD è possibile definire una vista assonometrica isometrica mediante il comando PVISTA.

Comando: PVISTA
Direzione vista corrente: VIEWDIR=1.00,1.00,1.00
Specificare un punto di vista o [Ruota] <Visualizza bussola e tre assi>: 1,1,1

Il comando visualizza nella prima riga le coordinate della vista corrente e chiede la specifica del punto di vista in coordinate assolute. Se si preme INVIO viene presentata la bussola per la definizione del punto di vista.
Se si digita l'opzione R si passa alla definizione del punto di vista in coordinate sferiche.
Finestra per definire il punto
di vista


 
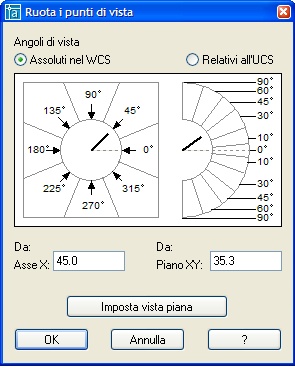
Finestra Ruota punti di vista che si attiva col menu Visualizza | Punti di vista 3D | Ruota i punti di vista. Nei due quadranti è possibile definire gli angoli di vista in pianta, a partire dall'asse X, considerato angolo 0, e in altezza, dal piano XY con angoli che vanno da -90° a + 90° passando per l'angolo 0 che corrisponde alla vista frontale.